A Minimal Example of Double Descent

The double descent phenomenon (Belkin et al. 2018, Nakkiran et al. 2019) has received significant attention in recent years and has been shown to be a common occurrence in various architectures, datasets, and training paradigms. In this demonstration, we illustrate the double descent phenomenon in an extremely simple setup: solving a ridge regression problem with six 2-dimensional data points projected into high-dimensional space.

To reproduce the results, visit the GitHub repository here.

Setup

We randomly generate a total of 12 data points, using $N=6$ for training and the remaining 6 for testing. Each data point has two features, and they form two clusters that are linearly separable. We represent the training data as $\mathbf{X}\in {\mathbb{R}}^{6\times 2}$.

We employ a random feature model with tanh features. Two random matrices are initialized: ${\mathbf{W}}_0\in {\mathbb{R}}^{D\times P}$ from $\mathcal{N}\left(0,\frac{1}{\sqrt{D}}\right)$ and ${\mathbf{W}}_1\in {\mathbb{R}}^{P\times C}$. The random features are computed as follows:

$$\mathbf{Z}=\tanh (\mathbf{X}\cdot {\mathbf{W}}_0).$$

Here, $P$, $D$, and $C$ represent the input feature dimension, the projected dimension, and the number of classes, respectively.

The ridge regression problem is solved in closed form:

$${\mathbf{W}}_1=({\mathbf{Z}}^T\mathbf{Z}+\alpha I{)}^{-1}{\mathbf{Z}}^T\mathbf{y}.$$

Visualizing the Peaking Phenomenon

In the figure below, we visualize the test error, MSE loss, condition number (the ratio of the maximum to the minimum singular values of $\mathbf{Z}$), and the norm of the solution ${\mathbf{W}}_1$ as functions of the overparameterization ratio $P/N$.

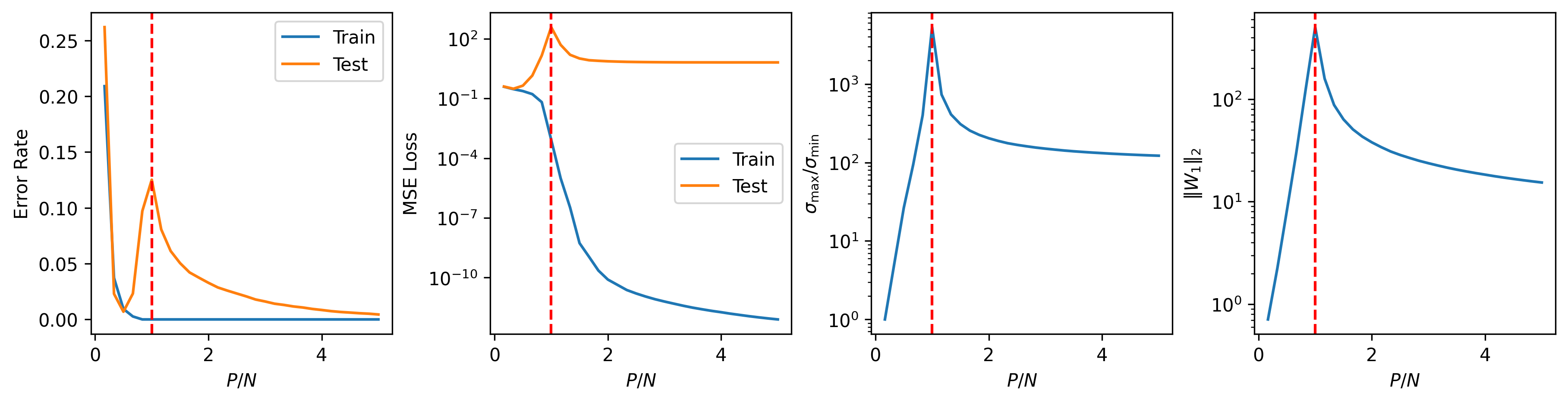
A clear peaking phenomenon is observed in all four metrics at $P/N=1$, highlighted by the red dashed line. Due to its simplicity, this example could potentially be used to demonstrate the double descent phenomenon in a classroom setting or to test new ideas.

For more details regarding the condition number and the role of optimization in the double descent phenomenon, please refer to Poggio et al. 2019 and a recent paper by Liu and Flanigan (2023) (link). In the latter, we demonstrate how different components of the optimization process influence the shape of the double descent curve.

References

[1] Belkin, M., Hsu, D., Ma, S., & Mandal, S. (2019). Reconciling modern machine-learning practice and the classical bias–variance trade-off. Proceedings of the National Academy of Sciences, 116(32), 15849-15854.

[2] Nakkiran, P., Kaplun, G., Bansal, Y., Yang, T., Barak, B., & Sutskever, I. (2021). Deep double descent: Where bigger models and more data hurt. Journal of Statistical Mechanics: Theory and Experiment, 2021(12), 124003.

[3] Poggio, T., Kur, G., & Banburski, A. (2019). Double descent in the condition number. arXiv preprint arXiv:1912.06190.

[4] Liu, C. Y., & Flanigan, J. (2023, December). Understanding the Role of Optimization in Double Descent. In OPT 2023: Optimization for Machine Learning.